 |
Sは他に別種のSやSがある訳ではないのでよいが、C及びCでは、それぞれその頂角や底面の形に無限の連続的変化があり、しかもそれらの変化は直ちにC及びCの形体種別に関係するので、これをどう処理するかということは大事な問題になってくる。かりに底面を円と決め、頂角を0°、30°、60°、90°、120°、180°の6種としぼっても先の13状態とこの6種で
に入れて計算すれば936種の図が必要になり、これにS、Sを加えると1548種にもなってしまう。これを一つ一つ追っていたのでは、かえって変化の総体が把握しにくくなるので、これは次のような方向に考えを転換して観察すればよいと思う。先づ
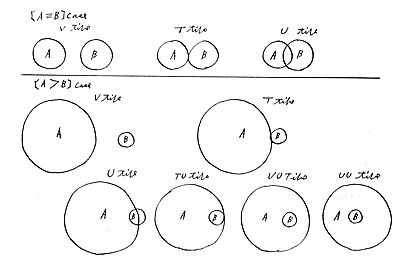
S、C、はS及びCに同じと置いて、一個のSと一個のCについての全関係を、第一には、一個のSを一定に置いて、任意の一対のC（頂点と母線を共有するC）の頂点の位置によって分類する。そうすると、Cの種類の多様性の問題は消去されて、一個のSと一個の点との関係になり、先のV、T、及びUU、VU、の4tipeだけが生じ、単純になる。この4tipeのそれぞれの任意点に於て、それぞれの一対のCの向きを全空間的に変えれば、一個のSに対する一対のCの全関係を、スッキリした姿で連続的に追うことが可能になる。〔第2図〕第二には、その逆である。即ち一対のCを固定しておき、これに合同なSの中心を移動して、その相関々係を分類する。この場合SはCに対し、V、T、TU、VU、UU、等の位置をとるから、それらの任意の位置で、さまざまの同心球を描くことによって、一個のCに対する、任意のSの全関係が第一の場合と同様に楽々と連続的に把握される。〔第3図〕
第三には、CとCとの関係の追求であるが、これも先づ合同な二つの一対のCの関係を取り上げる。二つの合同なCのそれぞれの軸（頂点を含む）のU、T、V、を中心にして、母線と母線、軸と軸、軸と母線のU、T、Vや、平行関係により、いくつかのtipeに分類して観察した後、垂直、その他自由な空間方向に頂点の位置で連続的に廻転して調査する。〔第4図〕
第四に合同でないCとCの関係を、類似なもの、対比なものについて、第三の位置で追求して行けばよい。〔第5図・第6図〕
充分単純化されてはいるものの、以上述べた方法は、やはり限りもなく複雑な分析のルートを提示したように見えるかも知れない。しかし事実は、わづかに二個の形体の相関々係に止っているのであって、これを三個、四個、五個、と増加して行けば六個までで、おどろくなかれ1235520種もの選択された図が必要となってくる。これらは、有機化合物の分子式や示性式等をはるかに越えた複雑な形体基本法則の、しかもほんの側面が見えている訳である。
1965、2、10 記
【参考文献】
特にあげるようなものはない。数学関係、特に幾何学関係の多くの文献、岩波数学辞典、エンサイクロペディアブリタニカ等を参考にした。
