完了形の構成 矢野目　鋼

PAGE | 1 | 2 | 3 |

ここまでは平面的を問題であったが、ふたたび発端にかえり、しかし次元は一つ進めて三次元の立方体を単元とし出発点とするところの系統的構造的な形の組成方法の試みに入ろう。「構成第III類」という教科としては立体的構造体の方が課題の重心になるのだが、結合の式そのた発展の過程はさきの正方形を単位とする形の場合とまったく同じであるので、このあとの説明は簡単になる。 　正方形は連結する等長の4つの辺と4つの直角とからなり、立方体は連結する同等の6つの正方形をもって閉じた、8つの頂点をもつ形であることは「正六面体」という名の示すとおりである。そして、正方形から立方体への発展的関係を措定することは一見して自明のことのようにおもわれる。しかしそれをそのように発端とする根拠を言うとなると、さきにものべたようにいまのところわたくしにとっては、形而上学的をまたは神がかった美辞の宇宙にさまよいこむことを免かれて、なんらかの意味あることを言うのは非常にむつかしい。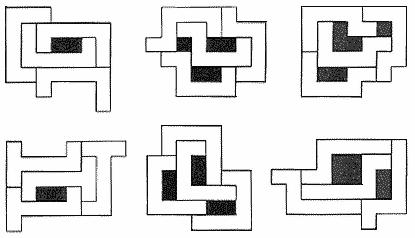 　ここからは、同等の立方体の連接結合を形の基底とするので、さきの正方形によるn正連形というコトバのかわりに、n立連形ということにする。平面の正連形における接合はタテかヨコかの2方向であったのに対して、立連形ではタテ、ヨコ、タカサの3方向に接合するので、ひとつのオーダーに属する形の数は当然に大きくなる。また、単位形の配置が対称的になって2個でもって対をなす形が多くでてくるが、一方を回転すれば他方と同等になる形の場合には、平面の正連形の場合に裏がえして同じものは同じとして消したように、一方を消去して員数に入れないこととし、そして、両手の手袋のように、回転しても一方が他方と同等にはならない対のあるときは、それらは互に異るものとして扱い、その両方を員数に加える。このように形の数はどんどん増殖するので、紙上のスケッチをもってしても、また木片を切って作った数百個のサイコロを利用しても、その形の数をかぞえたてて照合し確認することが事実上教室では技術的に困難となり、平面の場合に比較してその信頼度は早く低下する。具体的に実施されたところからいうと、5のオーダーにおいて29のちがった要素配置の立連形が確かめられたが、6のオーダーにおよんでは、紙上のスケッチによってさえ100を超えてなお増加するので、上記のような技術的困難さから、6立連形に属する形をすべてつくし、順序よく配列して確認することは、7以上のオーダーについても同様に、あきらめた。5のオーダー以下については、すべての形を確認し整序することは可能であり容易である。

次に、第二の結合式によってできる構造体に関しては、さきに示したように、平面の正連形の場合に4連結合を成立させる最低のオーダーは8であり、8正連形に属するもののうち数少い8種の形においてそれの成功が発見され、第9番にくるものはたぶんないだろうという結論があったが、立連形の場合には、4連結合は2のオーダーにおいてでてきてしまう。すなわち、2単位からなる角柱状の形を2個並べて接合したものを2組みつくり、それを「♯」の字型に積みかさねればよい。そして、6のオーダーに属するいくつかの形は8連結合を満足に成立させることがわかり、またどのオーダーの中にも、2連、3連、4連といった少い数の結合に止まる形がいくつかづつあって、低いオーダーには低次の結合、高いオーダーには高次の結合というようを傾向的に判然とした分類ができるようにはみえない。従って、さきの平面の場合のように、n連結合を成立させる最低のオーダーを求めるといった方法は、目標としての明瞭さが充分ではないといわねばならない。しかし6のオーダーにおける8連結合の成立は、このような構造の過程における一つの主要な段落を画するということは認めてよいようにおもわれる。そして5のオーダーによっては6連結合が最高らしく、6のオーダーによっては8連結合が最高らしいといった限度はあるので、二つの式をくずさないで得られる、そのオーダーにおける最高次の連結を求めることをもって一つの目標とするのがよいと考える。教室においては、9のオーダーによる少数の10連結合の例や10のオーダーによる少数の10連結合に成功した例があらわれ、それらのモデルが製作された。なお積極的な見通しをもってそれ以上のオーダーに進むことはいまのところ考えていない。その理由の一つは、消極的には、目標の明瞭さそのたで考察したところにかかわっており、すなわち立方体というものが一見簡明なようで、実は教室のわれわれにとっては複雑すぎるともいえる問題をその性質の中に含んでいることと、第二に、積極的にはいくつかの数少い典型的を組み立ての様式のあることが認められ、それ以上探究する必要はないようにおもわれるからである。